26. 树的子结构
题目描述:输入两棵二叉树 A 和 B,判断 B 是不是 A 的子结构。(约定空树不是任意一个树的子结构)
解题思路:先序遍历,包含判断。
public boolean isSubStructure(TreeNode A, TreeNode B) {
if (A == null || B == null) return false;
return isSameTree(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
}
public boolean isSameTree(TreeNode A, TreeNode B) {
if (B == null) return true;
if (A == null) return false;
if (A.val != B.val) return false;
return isSameTree(A.left, B.left) && isSameTree(A.right, B.right);
}
27. 二叉树的镜像
题目描述:完成一个函数,输入一个二叉树,该函数输出它的镜像。
例如输入:
4
/ \
2 7
/ \ / \
1 3 6 9
镜像输出:
4
/ \
7 2
/ \ / \
9 6 3 1
public TreeNode mirrorTree(TreeNode root) {
if (root == null) return null;
TreeNode temp = root.left;
root.left = mirrorTree(root.right);
root.right = mirrorTree(temp);
return root;
}
28. 对称的二叉树
题目描述:如果一个二叉树同此二叉树的镜像是同样的,定义其为对称的。
public boolean isSymmetric(TreeNode root) {
if (root == null) return true;
return isSame(root.left, root.right);
}
public boolean isSame(TreeNode A, TreeNode B) {
if (A == null && B == null) return true;
if (A == null || B == null || A.val != B.val) return false;
return isSame(A.right, B.left) && isSame(A.left, B.right);
}
29. 顺时针打印矩阵
题目描述:输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字。
解题思路:模拟、设定边界。
public int[] spiralOrder(int[][] matrix) {
if (matrix.length == 0) return new int[0];
int m = matrix.length, n = matrix[0].length;
int[] ans = new int[m * n];
int r1 = 0, r2 = matrix.length - 1, c1 = 0, c2 = matrix[0].length - 1;
int index = 0;
while (r1 <= r2 && c1 <= c2) {
for (int i = c1; i <= c2; i++) {
ans[index++] = matrix[r1][i];
}
for (int i = r1 + 1; i <= r2; i++) {
ans[index++] = matrix[i][c2];
}
if (r1 != r2) {
for (int i = c2 - 1; i >= c1; i--) {
ans[index++] = matrix[r2][i];
}
}
if (c1 != c2) {
for (int i = r2 - 1; i > r1; i--) {
ans[index++] = matrix[i][c1];
}
}
r1++; r2--; c1++; c2--;
}
return ans;
}
30. 包含 min 函数的栈
题目描述:定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为$O(1)$)。
解题思路:定义一个存储栈中当前最小元素的辅助栈。
Stack<Integer> mainStack;
Stack<Integer> minStack;
public MinStack() {
mainStack = new Stack<>();
minStack = new Stack<>();
}
public void push(int x) {
mainStack.push(x);
minStack.push(minStack.isEmpty() ? x : Math.min(minStack.peek(), x));
}
public void pop() {
mainStack.pop();
minStack.pop();
}
public int top() {
return mainStack.peek();
}
public int min() {
return minStack.peek();
}
31. 栈的压入、弹出序列
题目描述:输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列 1,2,3,4,5 是某栈的压入顺序,序列 4,5,3,2,1 是该压栈序列对应的一个弹出序列,但 4,3,5,1,2 就不可能是该压栈序列的弹出序列。
解题思路:模拟栈的压入与弹出过程。
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack<Integer> stack = new Stack<>();
for (int i = 0, j = 0; i < pushed.length; i++) {
stack.push(pushed[i]);
while (!stack.isEmpty() && stack.peek() == popped[j]) {
stack.pop();
j++;
}
}
return stack.isEmpty();
}
32.1 从上往下打印二叉树
题目描述:从上到下打印出二叉树的每个节点,同一层的节点按照从左到右的顺序打印。
解题思路:层次遍历。
public int[] levelOrder(TreeNode root) {
if (root == null) return new int[0];
Queue<TreeNode> queue = new LinkedList<>();
List<Integer> ans = new ArrayList<>();
queue.offer(root);
while(!queue.isEmpty()) {
int len = queue.size();
while (len-- > 0) {
TreeNode cur = queue.poll();
if (cur.left != null) queue.offer(cur.left);
if (cur.right != null) queue.offer(cur.right);
ans.add(cur.val);
}
}
int[] ansArray = new int[ans.size()];
for (int i = 0; i < ans.size(); i++) {
ansArray[i] = ans.get(i);
}
return ansArray;
}
32.2 从上往下打印二叉树II
题目描述:从上到下按层打印二叉树,同一层的节点按从左到右的顺序打印,每一层打印到一行。
解题思路:层次遍历。
public List<List<Integer>> levelOrder(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if(root != null) queue.add(root);
while(!queue.isEmpty()) {
List<Integer> tmp = new ArrayList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
tmp.add(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
res.add(tmp);
}
return res;
}
32.3 从上往下打印二叉树III
题目描述:请实现一个函数按照之字形顺序打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右到左的顺序打印,第三行再按照从左到右的顺序打印,其他行以此类推。
解题思路:层次遍历。
public List<List<Integer>> levelOrder(TreeNode root) {
Queue<TreeNode> queue = new LinkedList<>();
List<List<Integer>> res = new ArrayList<>();
if(root != null) queue.add(root);
while(!queue.isEmpty()) {
List<Integer> tmp = new ArrayList<>();
for(int i = queue.size(); i > 0; i--) {
TreeNode node = queue.poll();
tmp.add(node.val);
if(node.left != null) queue.add(node.left);
if(node.right != null) queue.add(node.right);
}
if(res.size() % 2 == 1) Collections.reverse(tmp);
res.add(tmp);
}
return res;
}
33. 二叉搜索树的后续遍历序列
题目描述:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。假设输入的数组的任意两个数字都互不相同。
解题思路:根据二叉搜索树的定义,可以通过递归,判断所有子树的 正确性 (即其后序遍历是否满足二叉搜索树的定义) ,若所有子树都正确,则此序列为二叉搜索树的后序遍历。最后一个节点为根节点,遍历数组从前向后找到第一个大于根节点的节点,如果该节点后面的所有节点均大于根节点,根节点满足二叉搜索树的定义,接着判断左子树与右子树是否满足条件。
public boolean verifyPostorder(int[] postorder) {
return recur(postorder, 0, postorder.length - 1);
}
boolean recur(int[] postorder, int i, int j) {
if(i >= j) return true;
int p = i;
while(postorder[p] < postorder[j]) p++;
int m = p;
while(postorder[p] > postorder[j]) p++;
return p == j && recur(postorder, i, m - 1) && recur(postorder, m, j - 1);
}
34. 二叉树中和为某一值的路径
题目描述:输入一颗二叉树的根节点和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
解题思路:典型的二叉树方案搜索问题,使用回溯法解决,其包含 先序遍历 + 路径记录 两部分。
LinkedList<List<Integer>> res = new LinkedList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> pathSum(TreeNode root, int sum) {
recur(root, sum);
return res;
}
void recur(TreeNode root, int tar) {
if(root == null) return;
path.add(root.val);
tar -= root.val;
if(tar == 0 && root.left == null && root.right == null)
res.add(new LinkedList(path));
recur(root.left, tar);
recur(root.right, tar);
path.removeLast();
}
35. 复杂链表的复制
题目描述:输入一个复杂链表(每个节点中有节点值,以及两个指针,一个指向下一个节点,另一个特殊指针指向任意一个节点),返回结果为复制后复杂链表的 head。
解题思路:将复制过程拆分为三个步骤:
- 复制每一个节点,使得复制后的节点都在当前节点的下一个节点
- 原生链表的节点的指向任意节点,使复制的节点也都指向某一任意节点
- 重新连接节点,把原生节点重新连接起来,把克隆后的节点连接起来
public Node copyRandomList(Node head) {
if (head == null) return null;
// 插入新节点
Node cur = head;
while (cur != null) {
Node clone = new Node(cur.val);
clone.next = cur.next;
cur.next = clone;
cur = clone.next;
}
// 建立 random 链接
cur = head;
while (cur != null) {
Node clone = cur.next;
if (cur.random != null)
clone.random = cur.random.next;
cur = clone.next;
}
// 拆分
cur = head;
Node pCloneHead = head.next;
while (cur.next != null) {
Node next = cur.next;
cur.next = next.next;
cur = next;
}
return pCloneHead;
}
36. 二叉搜索树与双向链表
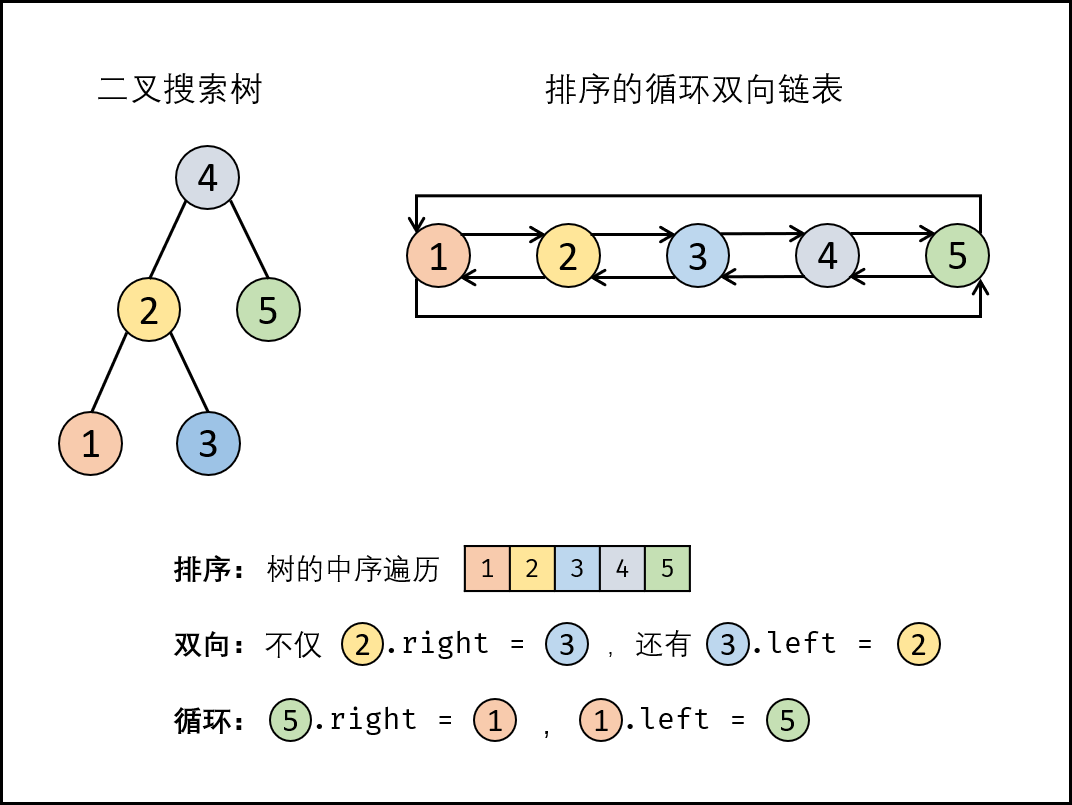
题目描述:输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
解题思路:将 二叉搜索树 转换成一个 “排序的循环双向链表” ,其中包含三个要素:
- 排序链表: 节点应从小到大排序,因此应使用 中序遍历 “从小到大”访问树的节点;
- 双向链表: 在构建相邻节点(设前驱节点
pre,当前节点cur)关系时,不仅应pre.right = cur,也应cur.left = pre; - 循环链表:设链表头节点
head和尾节点tail,则应构建head.left = tail和tail.right = head。
Node head, pre;
public Node treeToDoublyList(Node root) {
if (root == null) return null;
recur(root);
pre.right = head;
head.left = pre;
return head;
}
public void recur(Node root) {
if (root == null) return;
recur(root.left);
root.left = pre;
if (pre != null) {
pre.right = root;
} else {
head = root;
}
pre = root;
recur(root.right);
}
37. 序列化二叉树
题目描述:请实现两个函数,分别用来序列化和反序列化二叉树。
解题思路:前序遍历,使用空格分隔节点,用 # 表示空节点。
String deserializeStr;
public String serialize(TreeNode root) {
if (root == null) return "#";
return root.val + " " + serialize(root.left) + " " + serialize(root.right);
}
public TreeNode deserialize(String data) {
deserializeStr = data;
return deserialize();
}
public TreeNode deserialize() {
if (deserializeStr.length() == 0) return null;
int index = deserializeStr.indexOf(" ");
String node = index == -1 ? deserializeStr : deserializeStr.substring(0, index);
deserializeStr = index == -1 ? "" : deserializeStr.substring(index + 1);
if (node.equals("#")) return null;
int val = Integer.parseInt(node);
TreeNode t = new TreeNode(val);
t.left = deserialize();
t.right = deserialize();
return t;
}
38. 字符串的排列
题目描述:输入一个字符串,打印出该字符串中字符的所有排列。
输入:s = "abc"
输出:["abc","acb","bac","bca","cab","cba"]
解题思路:回溯法,注意可能有重复,需要去重。
List<String> res = new LinkedList<>();
char[] c;
public String[] permutation(String s) {
c = s.toCharArray();
dfs(0);
return res.toArray(new String[res.size()]);
}
void dfs(int x) {
if(x == c.length - 1) {
res.add(String.valueOf(c)); // 添加排列方案
return;
}
HashSet<Character> set = new HashSet<>();
for(int i = x; i < c.length; i++) {
if(set.contains(c[i])) continue; // 重复,因此剪枝
set.add(c[i]);
swap(c, i, x); // 交换,固定此位为 c[i]
dfs(x + 1); // 开启固定第 x + 1 位字符
swap(c, i, x); // 恢复交换
}
}
39. 数组中出现次数超过一半的数字
题目描述:数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。
输入: [1, 2, 3, 2, 2, 2, 5, 4, 2]
输出: 2
解题思路:摩尔投票法,正负抵消,将数组中出现次数超过一半的数字与其他数字抵消。
public int majorityElement(int[] nums) {
int x = 0, votes = 0;
for(int num : nums){
if(votes == 0) x = num;
votes += num == x ? 1 : -1;
}
return x;
}
40. 最小的 K 个数
题目描述:输入整数数组 arr ,找出其中最小的 k 个数。
输入:arr = [3,2,1], k = 2
输出:[1,2] 或者 [2,1]
解法一:快排。
public int[] getLeastNumbers(int[] arr, int k) {
if (k == 0 || arr.length == 0) {
return new int[0];
}
// 最后一个参数表示我们要找的是下标为k-1的数
return quickSearch(arr, 0, arr.length - 1, k - 1);
}
private int[] quickSearch(int[] nums, int lo, int hi, int k) {
// 每快排切分1次,找到排序后下标为j的元素,如果j恰好等于k就返回j以及j左边所有的数;
int j = partition(nums, lo, hi);
if (j == k) {
return Arrays.copyOf(nums, j + 1);
}
// 否则根据下标j与k的大小关系来决定继续切分左段还是右段。
return j > k? quickSearch(nums, lo, j - 1, k): quickSearch(nums, j + 1, hi, k);
}
// 快排切分,返回下标j,使得比nums[j]小的数都在j的左边,比nums[j]大的数都在j的右边。
private int partition(int[] nums, int lo, int hi) {
int v = nums[lo];
int i = lo, j = hi + 1;
while (true) {
while (++i <= hi && nums[i] < v);
while (--j >= lo && nums[j] > v);
if (i >= j) {
break;
}
int t = nums[j];
nums[j] = nums[i];
nums[i] = t;
}
nums[lo] = nums[j];
nums[j] = v;
return j;
}
解法二:最大堆。
public int[] getLeastNumbers(int [] nums, int k) {
if (k > nums.length || k < 0) return new int[0];
PriorityQueue<Integer> maxHeap = new PriorityQueue<>((o1, o2) -> o2 - o1);
for (int num : nums) {
maxHeap.add(num);
if (maxHeap.size() > k)
maxHeap.poll();
}
// 返回堆中的元素
int[] res = new int[maxHeap.size()];
int idx = 0;
for(int num: maxHeap) {
res[idx++] = num;
}
return res;
}
41.1 数据流中的中位数
题目描述:如何得到一个数据流中的中位数?如果从数据流中读出奇数个数值,那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值,那么中位数就是所有数值排序之后中间两个数的平均值。
解题思路:大顶推存储左面的元素,小顶堆存储右面的元素,这样就可以在 $O(1)$ 的时间找到中位数。
PriorityQueue<Integer> left = new PriorityQueue<>((o1, o2) -> o2 - o1);
PriorityQueue<Integer> right = new PriorityQueue<>();
int N = 0;
public void addNum(int num) {
if (N % 2 == 0) {
left.add(num);
right.add(left.poll());
} else {
right.add(num);
left.add(right.poll());
}
N++;
}
public double findMedian() {
if (N % 2 == 0)
return (left.peek() + right.peek()) / 2.0;
else
return (double) right.peek();
}
41.2 字符流中第一个不重复的字符
题目描述:请实现一个函数用来找出字符流中第一个只出现一次的字符。例如,当从字符流中只读出前两个字符 go 时,第一个只出现一次的字符是 g。当从该字符流中读出前六个字符 google 时,第一个只出现一次的字符是 l。
解题思路:使用字符数组记录每个字符出现的次数,每次插入时将字符放进队列中,并将重复的字符推出队列。
int[] cnts = new int[256];
Queue<Character> queue = new LinkedList<>();
public void insert(char ch) {
cnts[ch]++;
queue.offer(ch);
while (!queue.isEmpty() && cnts[queue.peek()] > 1) {
queue.poll();
}
}
public char firstAppearingOnce() {
return queue.isEmpty() ? '#' : queue.peek();
}
42. 连续子数组的最大和
题目描述:输入一个整型数组,数组里有正数也有负数。数组中的一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。
输入: nums = [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
解题思路:动态规划。定义状态 dp[i] 代表以元素 nums[i] 为结尾的连续子数组最大和;若 dp[i - 1] <= 0 说明 dp[i - 1] 对 dp[i] 产生负贡献,即 dp[i - 1] + nums[i] 还不如 nums[i] 本身大。
public int maxSubArray(int[] nums) {
if (nums == null || nums.length == 0) return 0;
int res = nums[0];
for (int i = 1; i < nums.length; i++) {
nums[i] += Math.max(nums[i - 1], 0);
res = Math.max(res, nums[i]);
}
return res;
}
43. 从 1 到 n 整数中 1 出现的次数
解题思路:找规律,从最高位计算到最低位。分类的思想,先求所有数中个位是 1 的个数,再求十位是 1 的个数,再求百位是 1 的个数…
假设 n = xyzdabc,此时求千位是 1 的个数,也就是 d 所在的位置,有以下三种情况:
d == 0,那么千位上1的个数就是xyz * 1000,前面有xyz中可能,后面abc有0 ~ 9991000 种可能;d == 1,那么千位上1的个数就是xyz * 1000 + abc + 1,abc的取值是0 ~ abc,所以要+1;d > 1,那么千位上1的个数就是xyz * 1000 + 1000;
public int countDigitOne(int n) {
int count = 0;
//依次考虑个位、十位、百位...是 1
for (long k = 1; k <= n; k *= 10) {
// xyzdabc
long abc = n % k;
long xyzd = n / k;
long d = xyzd % 10;
long xyz = xyzd / 10;
count += xyz * k;
if (d > 1) {
count += k;
}
if (d == 1) {
count += abc + 1;
}
}
return count;
}
44. 数字序列中某一位的数字
题目描述:数字以 0123456789101112131415… 的格式序列化到一个字符序列中。在这个序列中,第 5 位(从下标 0 开始计数)是 5,第 13 位是 1,第 19 位是4,等等。请写一个函数,求任意第 n 位对应的数字。
输入:n = 11
输出:0
解题思路:找规律。对于第 n 位对应的数字,令这个数字对应的数为 target,然后分三步进行:
- 首先找到这个数字对应的数是几位数,用 digits 表示;
- 然后确定这个对应的数的数值 target;
- 最后确定返回值是 target 中的哪个数字。

public int findNthDigit(int n) {
// 先判断 target 是几位数,用 digits 表示
int digits = 1;
while (n > digits * Math.pow(10, digits - 1) * 9) {
n -= digits * Math.pow(10, digits - 1) * 9;
digits++;
}
// 所在位置的数字
int target = (int)(Math.pow(10, digits - 1) + (n - 1) / digits);
// 数字中的第几位
return String.valueOf(target).charAt((n - 1) % digits) - '0';
}
45. 把数组排成最小
题目描述:输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。
输入: [3,30,34,5,9]
输出: "3033459"
解题思路:可以看成是一个排序问题,在比较两个字符串 S1 和 S2 的大小时,应该比较的是 S1+S2 和 S2+S1 的大小,如果 S1+S2 < S2+S1,那么应该把 S1 排在前面,否则应该把 S2 排在前面。
public String minNumber(int[] nums) {
String[] arr = new String[nums.length];
for (int i = 0; i < nums.length; i++) {
arr[i] = String.valueOf(nums[i]);
}
Arrays.sort(arr, (a,b) -> (a + b).compareTo(b + a));
String res = "";
for(int i = 0; i < arr.length; i++){
res += arr[i];
}
return res;
}
46. 把数字翻译成字符串
题目描述:给定一个数字,按照如下规则翻译成字符串:1 翻译成 a,2 翻译成 b… 26 翻译成 z。一个数字有多种翻译可能,例如 12258 一共有 5 种,分别是 abbeh,lbeh,aveh,abyh,lyh。实现一个函数,用来计算一个数字有多少种不同的翻译方法。
解题思路:动态规划,如果后两位数不满足两位数的条件(x > 9 && x < 26)只有一种情况,否则有两种情况,拆分成一位数和拆分成两位数。
public int translateNum(int num) {
if (num <= 9) return 1;
// xyzcba
int ba = num % 100;
if (ba <= 9 || ba >= 26) return translateNum(num / 10);
else return translateNum(num / 10) + translateNum(num / 100);
}
47. 礼物的最大价值
题目描述:在一个 m*n 的棋盘的每一个格都放有一个礼物,每个礼物都有一定价值(大于 0)。从左上角开始拿礼物,每次向右或向下移动一格,直到右下角结束。给定一个棋盘,求拿到礼物的最大价值。
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
解题思路:动态规划。设 f(i, j) 为从棋盘左上角走至单元格 (i,j) 的礼物最大累计价值,易得到以下递推关系:f(i,j) 等于 f(i,j−1) 和 f(i−1,j) 中的较大值加上当前单元格礼物价值 grid(i,j):
$f(i,j)=max[f(i,j−1),f(i−1,j)]+grid(i,j)$
由于 dp[i][j] 只与 dp[i−1][j] , dp[i][j−1] , grid[i][j] 有关系,因此可以将原矩阵 grid 用作 dp 矩阵,即直接在 grid 上修改即可。
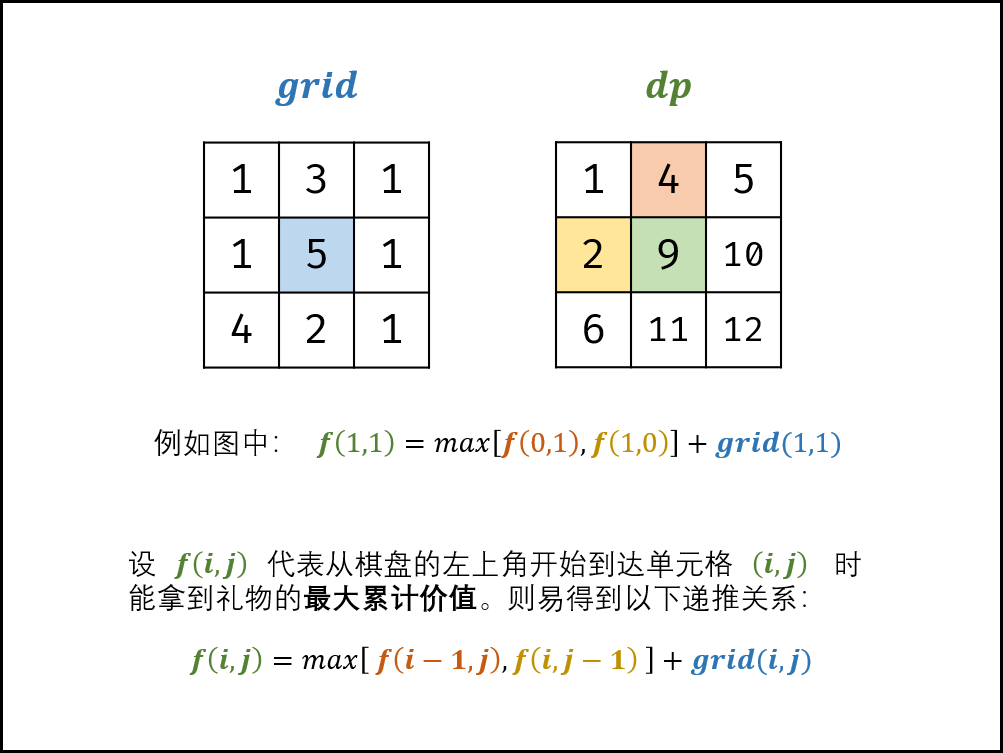
public int maxValue(int[][] grid) {
if (grid == null || grid.length == 0 || grid[0].length == 0) return 0;
int n = grid[0].length;
int[] dp = new int[n];
for (int[] value : grid) {
dp[0] += value[0];
for (int i = 1; i < n; i++)
dp[i] = Math.max(dp[i], dp[i - 1]) + value[i];
}
return dp[n - 1];
}