3. 数组中重复的数字
题目描述:在一个长度为 n 的数组里,所有的数字都在 0 ~ n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。找出数组中任意一个重复的数字。
输入:[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3
解题思路:首先可以考虑排序,先对原数组进行排序,之后遍历数组找到重复数字,时间复杂度 $O(nlogn)$,但这显然不是最优解;此外哈希表也能够解决,额外创建一个哈希表,将数组中的数字逐个放入哈希表中,只需遍历一次即可找到重复数字,时间复杂度 $O(n)$,额外空间复杂度 $O(n)$;
不过还有一种时间复杂度为 $O(n)$ 且额外空间复杂度为 $O(1)$ 的最优解法。
利用数组中的数字都在 0 ~ n-1 的范围内这一条件,如果数组中没有重复的数字,那么当数组排序后数字 i 都将会出现在下标为 i 的位置。如果有重复数字,就出现不止一个数字 i 出现在下标为 i 的位置,利用这一原理可以求解。

Java
public static int findRepeatNumber(int[] nums) {
if (nums == null || nums.length == 0) {
return -1;
}
for (int i = 0; i < nums.length; i++) {
while (nums[i] != i && nums[nums[i]] != nums[i]) {
swap(nums, i, nums[i]);
}
if (nums[i] != i) {
return nums[i];
}
}
return -1;
}
public static void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
Go
func findRepeatNumber(nums []int) int {
for idx, val := range nums{
if idx == val{
continue
}
if nums[val] == val{
return val
}
nums[val], nums[idx] = nums[idx], nums[val]
}
return 0
}
4. 二维数组中的查找
题目描述:在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
解题思路:从题目中可知,二维数组从左到右是递增的,从上到下也是递增的,那么如果我们从右上角作为起点,向左下方去找的话,就构成了一种二分结构,从图中可以看出,从右向左是递减的,从上到下是递增的,由此可得出三种情况:
- 目标值 > 当前值:接着向下找;
- 目标值 < 当前值:接着向左找;
- 目标值 = 当前值:数组中包含该整数,直接返回。


Java
public boolean findNumberIn2DArray(int[][] matrix, int target) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return false;
}
int i = 0, j = matrix[0].length - 1;
while (i < matrix.length && j >= 0) {
if (matrix[i][j] == target) {
return true;
}
if (target > matrix[i][j]) {
i++;
} else {
j--;
}
}
return false;
}
Go
func findNumberIn2DArray(matrix [][]int, target int) bool {
if len(matrix) == 0 {
return false
}
rows := 0
cols := len(matrix[0])-1
for rows < len(matrix) && cols >=0 {
if matrix[rows][cols] < target {
rows++
} else if matrix[rows][cols] > target{
cols--
} else {
return true
}
}
return false
}
5. 替换空格
题目描述:将字符串中的空格替换成”%20”。
输入:s = "We are happy."
输出:"We%20are%20happy."
解题思路:有两种比较好的解决方法,第一种是直接开辟一个新的数组,然后从前向后遍历,依次将原字符串中的字符添加进数组中,如果遇到空格,则添加 %20 三个字符,这种方法的时间复杂度为 $O(n)$,因为开辟了新的空间,额外空间复杂度也为 $O(n)$。
另外一种,空间复杂度为 $O(1)$,就是在字符串原有的基础上进行修改,首先遍历一遍字符串中的字符,统计出空格的数量,对应的将字符串的长度向后延长,预留出 %20 增加的位置。之后,使用双指针的方式从后向前遍历,指针 p1 的初始位置为字符串扩充前最后的位置, 指针 p2 的初始位置为扩充后最后的位置,两个指针同时向前滑动,如果 p1 指向的不是空格,则将改值赋到 p2 指向的位置;如果是空格,则将 p2 指向的位置以及前面两位分别赋上 %20 三个字符。直到指针 p2 到字符串的首位字符时结束遍历。

Java
public String replaceSpace(String s) {
StringBuilder sb = new StringBuilder(s);
int p1 = sb.length() - 1;
for (int i = 0; i <= p1; i++) {
if (sb.charAt(i) == ' ') {
sb.append(" ");
}
}
int p2 = sb.length() - 1;
while (p1 >= 0 && p2 > p1) {
char c = sb.charAt(p1--);
if (c == ' ') {
sb.setCharAt(p2--, '0');
sb.setCharAt(p2--, '2');
sb.setCharAt(p2--, '%');
} else {
sb.setCharAt(p2--, c);
}
}
return sb.toString();
}
Go
func replaceSpace(s string) string {
var str string
start := 0
for key,value := range s {
if value == ' '{
str += s[start:key]
str += "%20"
start = key+1
}
}
str += s[start:]
return str
}
6. 从尾到头打印链表
题目描述:输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。
输入:head = [1,3,2]
输出:[2,3,1]
解法一:递归
ArrayList<Integer> res = new ArrayList<>();
public int[] reversePrint(ListNode head) {
helper(head);
int[] ans = new int[res.size()];
for (int i = 0; i < res.size(); i++) {
ans[i] = res.get(i);
}
return ans;
}
public void helper(ListNode cur) {
if (cur == null) return;
helper(cur.next);
res.add(cur.val);
}
解法二:栈
Stack<Integer> stack = new Stack<>();
public int[] reversePrint(ListNode head) {
ListNode cur = head;
while(cur != null) {
stack.push(cur.val);
cur = cur.next;
}
int[] res = new int[stack.size()];
int index = 0;
while(!stack.isEmpty()) {
res[index++] = stack.pop();
}
return res;
}
7. 重建二叉树
题目描述:给定二叉树的先序与中序遍历,重建二叉树。
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
3
/ \
9 20
/ \
15 7
解题思路:二叉树先序遍历的第一个结点是根节点,找到其在中序遍历里的位置,二分。
public TreeNode buildTree(int[] preorder, int[] inorder) {
return helper(preorder, 0, inorder, 0, inorder.length);
}
public TreeNode helper(int[] preorder, int preIndex, int[] inorder, int inLeft, int inRight) {
if (preIndex >= preorder.length || inLeft == inRight) {
return null;
}
TreeNode root = new TreeNode(preorder[preIndex]);
for (int i = inLeft; i < inRight; i++) {
if (inorder[i] == preorder[preIndex]) {
root.left = helper(preorder, preIndex + 1, inorder, inLeft, i);
root.right = helper(preorder, preIndex + i - inLeft + 1, inorder, i + 1, inRight);
}
}
return root;
}
8. 二叉树的下一个结点
题目描述:给定一个二叉树和其中的一个结点,找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
解题思路:如果右结点不为空,则为右子树的最左结点;否则,为当前树的根结点,前提是当前结点为该左子树中的结点。
public TreeLinkNode GetNext(TreeLinkNode pNode) {
if (pNode.right != null) {
TreeLinkNode node = pNode.right;
while (node.left != null) {
node = node.left;
}
return node;
} else {
while (pNode.next != null) {
TreeLinkNode parent = pNode.next;
if (parent.left == pNode)
return parent;
pNode = pNode.next;
}
}
return null;
}
9. 用两个栈实现队列
解题思路:维护两个栈,每次入队列都存到 in 栈中,出队列从 out 栈出。
Stack<Integer> in = new Stack<Integer>();
Stack<Integer> out = new Stack<Integer>();
public void push(int node) {
in.push(node);
}
public int pop() throws Exception {
if (out.isEmpty())
while (!in.isEmpty())
out.push(in.pop());
if (out.isEmpty())
throw new Exception("queue is empty");
return out.pop();
}
10.1 斐波那契数列
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
public int fib(int n) {
if (n < 2) return n;
int a = 0, b = 1;
for (int i = 2; i <= n; i++) {
int sum = a + b;
a = b;
b = sum;
}
return b;
}
10.2 矩形覆盖
题目描述:我们可以用 2*1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2*1 的小矩形无重叠地覆盖一个 2*n 的大矩形,总共有多少种方法?
解题思路:归纳法能看出符合斐波那契数列。
public int RectCover(int target) {
if (target <= 2) return target;
int a = 1, b = 2;
for (int i = 3; i <= target; i++) {
int sum = a + b;
a = b;
b = sum;
}
return b;
}
10.3 跳台阶
题目描述:一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
解题思路:符合斐波那契数列。
public int numWays(int n) {
if (n == 0) return 1;
if (n <= 2) return n;
int a = 1, b = 2;
for (int i = 3; i <= n; i++) {
int sum = a + b;
a = b;
b = sum;
}
return b;
}
10.4 变态跳台阶
题目描述:一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级……它也可以跳上 n 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
解法一:每个台阶可以看做一块木板,让青蛙跳上去,n 个台阶就有 n 块木板,最后一块木板是青蛙达到的目的地,必须存在,其他 n-1 块木板可以任意选择是否存在,即每个木板有存在和不存在两种选择,n-1 块木板就有 $2^{n-1}$ 种跳法。
public int jumpFloor(int target) {
if (target <= 0) return 0;
return (int) Math.pow(2, target -1);
}
解法二:动态规划,上一题普通跳台阶种,跳到台阶 n 的跳法为跳到 n-1 和 n-2 两个台阶跳法之和,而本题没有限制青蛙最多能向上跳几阶台阶,所以跳到台阶 n 的跳法为前面所有跳法之和。
public int JumpFloor(int target) {
int[] dp = new int[target];
Arrays.fill(dp, 1);
for (int i = 1; i < target; i++) {
for (int j = 0; j < i; j++) {
dp[i] += dp[j];
}
}
return dp[target - 1];
}
11. 旋转数组的最小数字
题目描述:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
输入:[3,4,5,1,2]
输出:1
解题思路:二分查找,如果找数组中的最小数字,只需要遍历一下数组就可以了,但是这道题我们要利用上旋转数组这一条件。数组在没有旋转之前是一个递增数组,也就是下标小的元素一定小于或等于下标大的元素,那数组旋转之后就打破了这一特性,可以利用二分查找寻找哪一边不符合左边的元素小于右边的元素,那最小数字一定在那一边,如果不确定在哪一边,就将有临界向左挪一位。
public int minArray(int[] numbers) {
int left = 0, right = numbers.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (numbers[mid] > numbers[right]) {
left = mid + 1;
} else if (numbers[mid] < numbers[right]) {
right = mid;
} else {
right--;
}
}
return numbers[left];
}
12. 矩阵中的路径
题目描述:判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向上下左右移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。
解题思路:深度优先搜索。
int[][] directions = { {0, 1}, {0, -1}, {1, 0}, {-1, 0} };
public boolean exist(char[][] board, String word) {
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
boolean flag = backtrack(board, word, 0, i, j, new boolean[board.length][board[0].length]);
if (flag) return true;
}
}
return false;
}
public boolean backtrack(char[][] board, String word, int index, int r, int c, boolean[][] marked) {
if (index == word.length()) {
return true;
}
if (r < 0 || c < 0 || r >= board.length || c >= board[0].length || marked[r][c] || word.charAt(index) != board[r][c]) {
return false;
}
marked[r][c] = true;
for (int[] direction: directions) {
boolean flag = backtrack(board, word, index + 1, r + direction[0], c + direction[1], marked);
if (flag) return true;
}
marked[r][c] = false;
return false;
}
13. 机器人的运动范围
题目描述:地上有一个 m 行和 n 列的方格。一个机器人从坐标 [0,0] 的格子开始移动,每一次只能向左,右,上,下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于 k 的格子。 例如,当 k 为 18 时,机器人能够进入方格 [35,37],因为 3+5+3+7=18。但是,它不能进入方格 [35,38],因为 3+5+3+8=19。请问该机器人能够达到多少个格子?
解题思路:深度优先搜索。
int[][] next = { {1, 0}, {-1, 0}, {0, 1}, {0, -1} };
int[][] digitSum;
int count = 0;
int rows, cols, threshold;
public int movingCount(int m, int n, int k) {
this.rows = m;
this.cols = n;
this.threshold = k;
initStatus(rows, cols);
boolean[][] marked = new boolean[rows][cols];
dfs(marked, 0, 0);
return count;
}
private void dfs(boolean[][] marked, int r, int c) {
if (r < 0 || r >= rows || c < 0 || c >= cols || marked[r][c]) return;
marked[r][c] = true;
if (digitSum[r][c] > threshold) return;
count++;
for (int[] n : next) {
dfs(marked, r + n[0], c + n[1]);
}
}
private void initStatus(int rows, int cols) {
int n = Math.max(rows, cols);
int[] digitSum = new int[n];
for (int i = 0; i < n; i++) {
int tmp = i;
while (tmp != 0) {
digitSum[i] += tmp % 10;
tmp /= 10;
}
}
this.digitSum = new int[rows][cols];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
this.digitSum[i][j] = digitSum[i] + digitSum[j];
}
}
}
14.1 剪绳子 I
题目描述:把一根绳子剪成多段,并且使得每段的长度乘积最大。
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
解题思路:动态规划
- 边界条件:
dp[1] = 1,表示长度为2的绳子最大乘积为1 - 状态转移方程:

public int cuttingRope(int n) {
int[] dp = new int[n + 1];
dp[1] = 1;
for (int i = 2; i <= n; i++)
for (int j = 1; j < i; j++)
dp[i] = Math.max(dp[i], Math.max(j * (i - j), dp[j] * (i - j)));
return dp[n];
}
14.2 剪绳子 II
题目描述:在上一题的基础上扩大了范围,答案需要取模 1e9+7 (1000000007)。
解题思路:本题如果使用 DP 难度就增大了,因为 long 已经不足以去存储中间结果的状态,因此只能使用 BigInteger 的方式去做。而此题更适合使用贪心算法去解决。
通过数学归纳可知,只有长度为 2 和 3 的绳子不应再切分,且 3 比 2 更优。
public int cuttingRope(int n) {
if(n == 2) return 1;
if(n == 3) return 2;
int mod = (int)1e9 + 7;
long res = 1;
while(n > 4) {
res *= 3;
res %= mod;
n -= 3;
}
return (int)(res * n % mod);
}
15. 二进制中 1 的个数
题目描述:输入一个整数,输出该数二进制表示中 1 的个数。其中负数用补码表示。
输入:00000000000000000000000000001011
输出:3
解题思路:利用 n & (n - 1) 操作的特性,将最右边的 1 变为 0。
(n−1): 二进制数字n最右边的1变成0,此1右边的0都变成1。n & (n - 1): 二进制数字n最右边的1变成0,其余不变。
public int hammingWeight(int n) {
int count = 0;
while (n != 0) {
n = n & (n - 1);
count++;
}
return count;
}
16. 数值的整数次方
题目描述:给定一个 double 类型的浮点数 base 和 int 类型的整数 exponent,求 base 的 exponent 次方。
输入: 2.00000, 10
输出: 1024.00000
解题思路:经典位运算快速幂算法。
public double myPow(double x, int n) {
if (x == 0) return 0;
if (n < 0) {
x = 1 / x;
n = -n;
}
double res = 1;
while (n != 0) {
if ((n & 1) == 1) {
res *= x;
}
x *= x;
n /= 2;
}
return res;
}
17. 打印从 1 到最大的 n 位数
题目描述:输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数即 999。
解题思路:题目没有说明数据位数范围,应按照大数问题(超出编程语言自带的数据结构表示范围)处理。
public void print1ToMaxOfNDigits(int n) {
if (n <= 0)
return;
char[] number = new char[n];
print1ToMaxOfNDigits(number, 0);
}
private void print1ToMaxOfNDigits(char[] number, int digit) {
if (digit == number.length) {
printNumber(number);
return;
}
for (int i = 0; i < 10; i++) {
number[digit] = (char) (i + '0');
print1ToMaxOfNDigits(number, digit + 1);
}
}
private void printNumber(char[] number) {
int index = 0;
while (index < number.length && number[index] == '0')
index++;
while (index < number.length)
System.out.print(number[index++]);
System.out.println();
}
18.1 在 O(1) 时间内删除链表节点
题目描述:给定单向链表的头指针和一个要删除的节点的值,定义一个函数删除该节点。
输入: head = [4,5,1,9], val = 5
输出: [4,1,9]
解题思路:如果该节点不是尾节点,那么可以直接将下一个节点的值赋给该节点,然后令该节点指向下下个节点,再删除下一个节点,时间复杂度为 $O(1)$;否则,就需要先遍历链表,找到节点的前一个节点,然后让前一个节点指向 null,时间复杂度为 $O(N)$。
public ListNode deleteNode(ListNode head, ListNode tobeDelete) {
if (head == null || tobeDelete == null)
return null;
if (tobeDelete.next != null) {
// 要删除的节点不是尾节点
ListNode next = tobeDelete.next;
tobeDelete.val = next.val;
tobeDelete.next = next.next;
} else {
if (head == tobeDelete)
// 只有一个节点
head = null;
else {
ListNode cur = head;
while (cur.next != tobeDelete)
cur = cur.next;
cur.next = null;
}
}
return head;
}
18.2 删除链表中重复的结点
题目描述:在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针。
解题思路:递归的思想,每次删除一个重复的节点。
public ListNode deleteDuplication(ListNode pHead) {
if (pHead == null || pHead.next == null)
return pHead;
ListNode next = pHead.next;
if (pHead.val == next.val) {
while (next != null && pHead.val == next.val)
next = next.next;
return deleteDuplication(next);
} else {
pHead.next = deleteDuplication(pHead.next);
return pHead;
}
}
19. 正则表达式匹配
题目描述:请实现一个函数用来匹配包括 . 和 * 的正则表达式。模式中的字符 . 表示任意一个字符,而 * 表示它前面的字符可以出现任意次(包含 0 次)。
输入:
s = "aa"
p = "a*"
输出: true
解题思路:动态规划
-
定义状态
dp[i][j]:s的前i个字符能够匹配p的前j个字符,注意这里的范围是(]的,即(0, i]与(0, j]。 -
转移方程:
- 若主串字符与正则串字符相等,或者正则串的字符为
.,则 $dp[i][j] = dp[i - 1][j - 1]$ - 若正则串字符为
*,可能有两种情况:- 正则串表示
0个字符,直接砍掉正则串的后面两个, $dp[i][j] = dp[i][j-2]$ - 正则串表示当前字符出现多次,正则串不动,主串向前移动一位,$dp[i][j] = dp[i-1][j]$
- 正则串表示
- 若主串字符与正则串字符相等,或者正则串的字符为
public boolean isMatch(String s, String p) {
int m = s.length, n = p.length;
boolean[][] dp = new boolean[m + 1][n + 1];
// 空主串与空模式串匹配
dp[0][0] = true;
// 空主串与非空模式串
for (int i = 1; i <= n; i++) {
if (p.charAt(i - ) == '*') {
dp[0][i] = dp[0][i - 2];
}
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
// 字符相等
if (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.') {
dp[i][j] = dp[i - 1][j - 1];
} else if (p.charAt(j - 1) == '*') {
if (p.charAt(j - 2) == s.charAt(i - 1) || p.charAt(j - 2) == '.') {
dp[i][j] |= dp[i - 1][j]; // a* 表示出现多次
dp[i][j] |= dp[i][j - 2]; // a* 表示出现 0 次
} else {
dp[i][j] = dp[i][j - 2]; // a* 表示出现 0 次
}
}
}
}
return dp[m][n];
}
20. 表示数值的字符串
题目描述:实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串 +100、5e2、-123、3.1416 和 -1E-16 都表示数值。 但是 12e、1a3.14、1.2.3、+-5 和 12e+4.3 都不是。
解法一:正则表达式
public boolean isNumber(String s) {
if (s == null || s.length() == 0) return false;
return s.trim().matches("[+-]?([0-9]+(\\.[0-9]*)?|\\.[0-9]+)(e[+-]?[0-9]+)?");
}
解法二:条件判断
public boolean isNumber(String s) {
if(s == null || s.length() == 0) return false;
// 标记是否遇到相应情况
boolean numSeen = false;
boolean dotSeen = false;
boolean eSeen = false;
char[] str = s.trim().toCharArray();
for(int i = 0;i < str.length; i++) {
if(str[i] >= '0' && str[i] <= '9'){
numSeen = true;
} else if(str[i] == '.'){
// .之前不能出现.或者e
if(dotSeen || eSeen){
return false;
}
dotSeen = true;
} else if(str[i] == 'e' || str[i] == 'E') {
// e之前不能出现e,必须出现数
if(eSeen || !numSeen){
return false;
}
eSeen = true;
numSeen = false;// 重置numSeen,排除123e或者123e+的情况,确保e之后也出现数
} else if(str[i] == '-' || str[i] == '+') {
// +-出现在0位置或者e/E的后面第一个位置才是合法的
if(i != 0 && str[i-1] != 'e' && str[i-1] != 'E'){
return false;
}
} else{// 其他不合法字符
return false;
}
}
return numSeen;
}
21. 调整数组顺序使奇数位于偶数前面
题目描述:需要保证奇数和奇数、偶数和偶数之间的相对位置不变。
解题思路:Leetcode 上的题目没有要求相对顺序不变,可以用双指针解决,双指针的基本操作。
public int[] exchange(int[] nums) {
int oddCount = 0;
for (int x : nums) {
if (x % 2 == 1) oddCount++;
}
int[] copy = nums.clone();
int i = 0, j = oddCount;
for (int x : copy) {
if (x % 2 == 1) nums[i++] = x;
else nums[j++] = x;
}
return nums;
}
22. 链表中倒数第 K 个节点
题目描述:输入一个链表,输出该链表中倒数第 k 个节点。
给定一个链表: 1->2->3->4->5, 和 k = 2.
返回链表 4->5.
解题思路:快慢指针,p1 指针先走到正数第 k 个节点,之后和 p2 一同向前移动,直到 p1 到达尾节点的后面,此时 p2 指向的正是到处第 k 个节点。
public ListNode getKthFromEnd(ListNode head, int k) {
ListNode p1 = head, p2 = head;
while (k-- > 0) {
p1 = p1.next;
}
while (p1 != null) {
p1 = p1.next;
p2 = p2.next;
}
return p2;
}
23. 链表中环的入口结点
题目描述:给一个链表,若其中包含环,请找出该链表的环的入口结点。
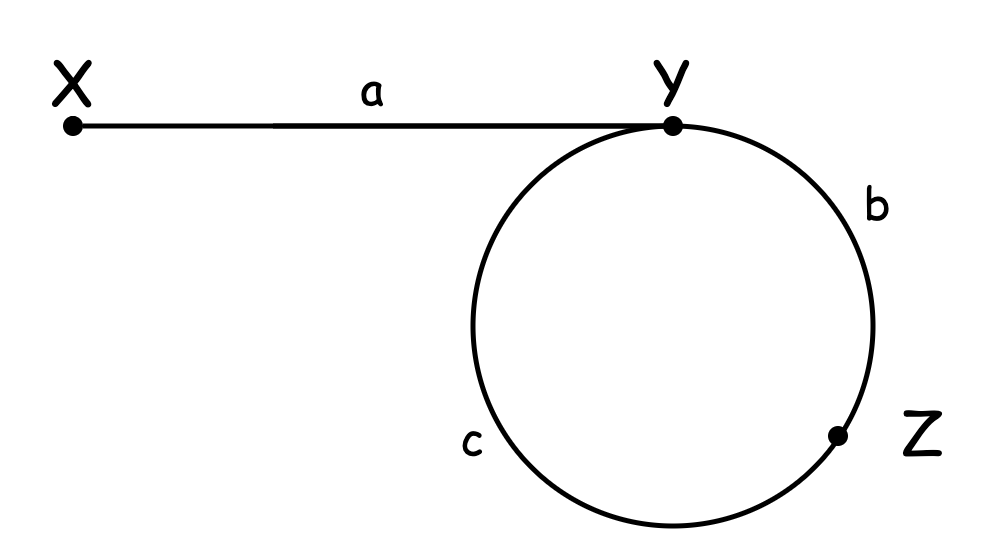
解题思路:假设链表头是 X,环的第一个节点是 Y,slow 和 fast 第一次的交点是 Z。各段的长度分别是 a,b,c。slow 每次向前走一个节点,fast 每次向前走两个结点,第一次相遇时 slow 走过的距离为 a+b,fast 走过的距离为 a+b+c+b,因为 fast 的速度是 slow 的两倍,所以 fast 走的距离是 slow 的两倍,由 2(a+b) = a+b+c+b 可得 a = c。这时,让两个指针分别从 X 和 Z 开始走,每次都走一步,那么正好会在 Y 相遇,也就是环的第一个节点。
public ListNode EntryNodeOfLoop(ListNode pHead) {
if (pHead == null || pHead.next == null)
return null;
ListNode slow = pHead, fast = pHead;
do {
fast = fast.next.next;
slow = slow.next;
} while (slow != fast);
fast = pHead;
while (slow != fast) {
slow = slow.next;
fast = fast.next;
}
return slow;
}
24. 反转链表
题目描述:定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。
方法一:递归
public ListNode reverseList(ListNode head) {
if (head == null || head.next == null) return head;
ListNode next = head.next;
head.next = null;
ListNode newHead = reverseList(next);
next.next = head;
return newHead;
}
方法二:头插法
public ListNode reverseList(ListNode head) {
ListNode newList = new ListNode(-1);
while (head != null) {
ListNode next = head.next;
head.next = newList.next;
newList.next = head;
head = next;
}
return newList.next;
}
25. 合并两个排序的链表
题目描述:输入两个递增排序的链表,合并这两个链表并使新链表中的节点仍然是递增排序的。
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
ListNode dummyNode = new ListNode(-1);
ListNode cur = dummyNode;
while (l1 != null && l2 != null) {
if (l1.val > l2.val) {
cur.next = l2;
l2 = l2.next;
} else {
cur.next = l1;
l1 = l1.next;
}
cur = cur.next;
}
cur.next = l1 != null ? l1 : l2;
return dummyNode.next;
}