组合数之和 IV
Leetcode - 337 Combination Sum IV (Medium)
题目描述:从数组 nums 中选出和为 target 的数字组合,数字之间的顺序不同表示不同的组合。
nums = [1, 2, 3]
target = 4
The possible combination ways are:
(1, 1, 1, 1)
(1, 1, 2)
(1, 2, 1)
(1, 3)
(2, 1, 1)
(2, 2)
(3, 1)
Note that different sequences are counted as different combinations.
Therefore the output is 7.
public int combinationSum4(int[] nums, int target) {
int[] dp = new int[target + 1];
dp[0] = 1;
for(int i = 1; i < dp.length; i++){
for(int j = 0; j < nums.length; j++){
if(i - nums[j] >= 0){
dp[i] += dp[i - nums[j]];
}
}
}
return dp[target];
}
唯一的二叉搜索树(BST)
Leetcode - 96 Unique Binary Search Trees (Medium)
题目描述:给定整数 n,计算由 1…n 能组成多少个不同的二叉搜索树。
Input: 3
Output: 5
Explanation:
Given n = 3, there are a total of 5 unique BST's:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
解题思路:这道题非常棒,从上述的输入示例中可以看出,如果 n = 3,最后输出的可能 BST 是分别由 1、2 和 3 作为根节点的 BST 数目之和。设 G(n) 为节点数为 n 时 BST 的数量,这也就是本题需要计算的结果。那么 G(n) 是怎么计算的呢? 设 F(i,n) 为当根节点是 i 时 BST 的数量,那么 G(n) 就可以分解成 G(n) = F(1,n) + F(2,n) +…+ F(n,n)。
问题又来了,F(i,n) 是怎么计算的? 假设给定序列 [1 2 3 4 5 6 7],F(3,7) 表示以 3 为根节点 BST 的数量,这时可以划分左子树与右子树,左子树由 [1 2] 组成,为 G(2);右子树由 [4 5 6 7] 组成,为 G(4),那么组合结果为 F(3,7) = G(2) * G(4),即 F(i,n) = G(i - 1) * G(n - i)。可以定义初始状态,当 n = 0 时,空树,G(0) = 1;当 n = 1 时,树中只有一个节点,G(1) = 1。
这样就可以用动态规划计算最终结果:G(n) = G(0) * G(n-1) + G(1) * G(n-2) +…+ G(n-1) * G(0)。
public int numTrees(int n) {
int [] G = new int[n + 1];
G[0] = G[1] = 1;
for(int i = 2; i <= n; i++) {
for(int j = 1; j <= i; j++) {
G[i] += G[j - 1] * G[i - j];
}
}
return G[n];
}
最大正方形
Leetcode - 221 Maximal Square (Medium)
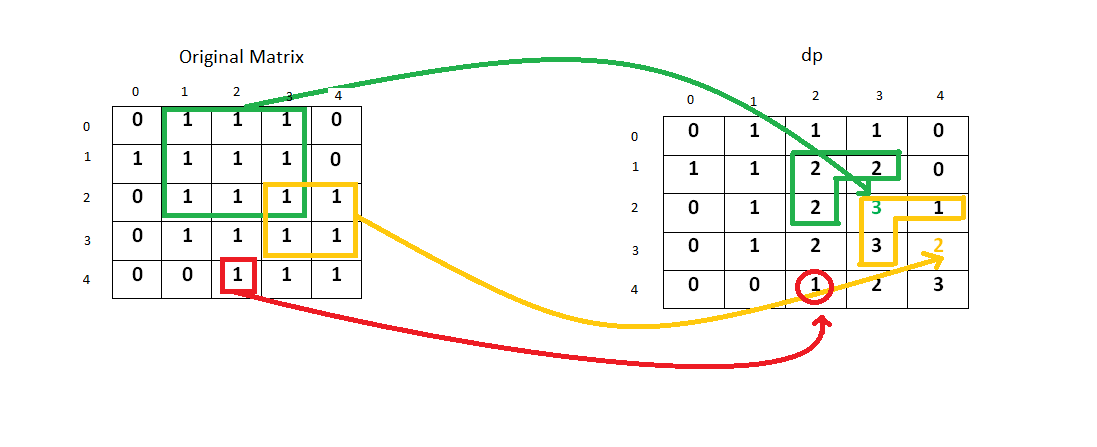
题目描述:找出矩阵中用 1 表示的最大正方形的面积。
Input:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
Output: 4
解题思路:d(i, j) 表示在索引为 i 和 j 时,最大正方形的边长,可以从图中看出,如果当前位置是 1, 最大边长就是左上方、上方与左方的最小值加 1,
$dp(i, j) = min(dp(i - 1, j), dp(i - 1, j - 1), dp(i, j - 1)) + 1$
public int maximalSquare(char[][] matrix) {
int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0;
int[][] dp = new int[rows + 1][cols + 1];
int maxsqlen = 0;
for (int i = 1; i <= rows; i++) {
for (int j = 1; j <= cols; j++) {
if (matrix[i-1][j-1] == '1'){
dp[i][j] = Math.min(Math.min(dp[i][j - 1], dp[i - 1][j]), dp[i - 1][j - 1]) + 1;
maxsqlen = Math.max(maxsqlen, dp[i][j]);
}
}
}
return maxsqlen * maxsqlen;
}
可以看出每次计算的 dp(i, j) 只与左上方、上方和左方的数值有关,所有可以用一维数组记录数据。
public int maximalSquare(char[][] matrix) {
int rows = matrix.length, cols = rows > 0 ? matrix[0].length : 0;
int[] dp = new int[cols + 1];
int maxsqlen = 0, prev = 0;
for (int i = 1; i <= rows; i++) {
for (int j = 1; j <= cols; j++) {
int temp = dp[j];
if (matrix[i - 1][j - 1] == '1') {
dp[j] = Math.min(Math.min(dp[j - 1], prev), dp[j]) + 1;
maxsqlen = Math.max(maxsqlen, dp[j]);
} else {
dp[j] = 0;
}
prev = temp;
}
}
return maxsqlen * maxsqlen;
}
完全平方数
Leetcode - 279 Perfect Squares (Medium)
题目描述:给定一个正整数,就算最少能由几个完全平方数组成。
Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.
解题思路:dp[n] 表示给定数为 n 时,完美平方数的最少数量。
dp[0] = 0
dp[1] = dp[0]+1 = 1
dp[2] = dp[1]+1 = 2
dp[3] = dp[2]+1 = 3
dp[4] = Min{ dp[4-1*1]+1, dp[4-2*2]+1 }
= Min{ dp[3]+1, dp[0]+1 }
= 1
dp[5] = Min{ dp[5-1*1]+1, dp[5-2*2]+1 }
= Min{ dp[4]+1, dp[1]+1 }
= 2
.
.
.
dp[13] = Min{ dp[13-1*1]+1, dp[13-2*2]+1, dp[13-3*3]+1 }
= Min{ dp[12]+1, dp[9]+1, dp[4]+1 }
= 2
.
.
.
dp[n] = Min{ dp[n - i*i] + 1 }, n - i*i >=0 && i >= 1
public int numSquares(int n) {
int[] dp = new int[n + 1];
Arrays.fill(dp, Integer.MAX_VALUE);
dp[0] = 0;
for(int i = 1; i <= n; ++i) {
int min = Integer.MAX_VALUE;
int j = 1;
while(i - j*j >= 0) {
min = Math.min(min, dp[i - j*j] + 1);
++j;
}
dp[i] = min;
}
return dp[n];
}
最长上升子序列
Leetcode - 300 Longest Increasing Subsequence (Medium)
Input: [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
解题思路:动态规划经典问题,dp[i] 表示前 i 个数以 A[i] 结尾的最长上升子序列长度。
$dp[i] = max(dp[j]) + 1, 0 <= j < i$
$LIS_{length} = max(dp[i]), 0 <= i < n$
public int lengthOfLIS(int[] nums) {
if(nums.length == 0) return 0;
int[] dp = new int[nums.length];
dp[0] = 1;
int maxAns = 1;
for(int i = 1; i < dp.length; i++){
int maxVal = 0;
for(int j = 0; j < i; j++){
if(nums[i] > nums[j]){
maxVal = Math.max(maxVal, dp[j]);
}
}
dp[i] = maxVal + 1;
maxAns = Math.max(maxAns, dp[i]);
}
return maxAns;
}
拆分词句
Leetcode - 139 Word Break (Medium)
题目描述:判断给定的字符串是否是有词库里的单词拼接而成的,词库中的单词都能够多次使用。
Input: s = "leetcode", wordDict = ["leet", "code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".
解题思路:dp[i] 表示前 i 个字符能否被拆分成词库中的单词,dp[n] 就是本题需要求解的结果。
public boolean wordBreak(String s, List<String> wordDict) {
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for(int i = 1; i <= s.length(); i++){
for(int j = 0; j < i; j++){
if(dp[j] && wordDict.contains(s.substring(j, i))){
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
三角形
Leetcode - 120 Triangle (Medium)
题目描述:给定一个三角形,寻找一条自上而下的路径,使得路径和最短,只能向下走相邻的节点。
解题思路: 每个节点记录从下到上的最短路径和。
dp[i] = min(triangle[j], triangle[j + 1]) + triangle[i][j]
public int minimumTotal(List<List<Integer>> triangle) {
int[] res = new int[triangle.size() + 1];
for (int i = triangle.size() - 1; i >= 0; i--) {
for (int j = 0; j < triangle.get(i).size(); j++) {
res[j] = Math.min(res[j], res[j + 1]) + triangle.get(i).get(j);
}
}
return res[0];
}
爬台阶
Leetcode - 70 Climbing Stairs (Easy)
题目描述:每次能爬一个或两个台阶,如果有 n 个台阶的话,计算爬到顶端的方法数量。
解题思路:dp(1) = 1 dp(2) = 2 dp(n) = dp(n - 1) + dp(n - 2)
public int climbStairs(int n) {
if(n <= 0) return 0;
if(n <= 2) return n;
int f1 = 1, f2 = 2;
for(int i = 3; i <= n; i++){
int t = f1 + f2;
f1 = f2;
f2 = t;
}
return f2;
}
最大乘积子序列
Leetcode - 152 Maximum Product Subarray (Medium)
Input: [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.
解题思路:记录从 0 到 i,每个 i 的最大乘积值与最小乘积值。
public int maxProduct(int[] nums) {
if(nums.length == 0) return 0;
int maxPre = nums[0];
int minPre = nums[0];
int max, min;
int maxSoFar = nums[0];
for(int i = 1; i < nums.length; i++){
max = Math.max(Math.max(maxPre * nums[i], minPre * nums[i]), nums[i]);
min = Math.min(Math.min(maxPre * nums[i], minPre * nums[i]), nums[i]);
System.out.println(max + " " + min);
maxSoFar = Math.max(max, maxSoFar);
maxPre = max;
minPre = min;
}
return maxSoFar;
}
最佳买卖股票的时间 I
Leetcode - 121 Best Time to Buy and Sell Stock (Easy)
题目描述:只能持有一只股票,一天只能买卖一次。
解法一:DP 解法
public int maxProfit(int[] prices) {
if(prices == null || prices.length == 0) return 0;
int[][] mp = new int[prices.length][3];
mp[0][1] = -prices[0];
int res = 0;
for (int i = 1; i < prices.length; i++){
mp[i][0] = mp[i - 1][0]; // 没有买卖
mp[i][1] = Math.max(mp[i - 1][1], mp[i - 1][0] - prices[i]); // 买了股票
mp[i][2] = mp[i - 1][1] + prices[i]; // 卖了股票
res = Math.max(res, Math.max(mp[i][0], Math.max(mp[i][1], mp[i][2])));
}
return res;
}
解法二:优解
public int maxProfit(int prices[]) {
int minprice = Integer.MAX_VALUE;
int maxprofit = 0;
for (int i = 0; i < prices.length; i++) {
if (prices[i] < minprice)
minprice = prices[i];
else if (prices[i] - minprice > maxprofit)
maxprofit = prices[i] - minprice;
}
return maxprofit;
}